Python priority queue -- heapq

This module provides an implementation of the heap queue algorithm, also known as the priority queue algorithm.

Heaps are binary trees for which every parent node has a value less than or equal to any of its children. This implementation uses arrays for which heap[k]<= heap[2*k+1] and heap[k] <= heap[2*k+2] for all k, counting elements from zero. For the sake of comparison, non-existing elements are considered to be infinite. The interesting property of a heap is that its smallest element is always the root, heap[0].

The API below differs from textbook heap algorithms in two aspects: (a) We use zero-based indexing. This makes the relationship between the index for a node and the indexes for its children slightly less obvious, but is more suitable since Python uses zero-based indexing. (b) Our pop method returns the smallest item, not the largest (called a “min heap” in textbooks; a “max heap” is more common in texts because of its suitability for in-place sorting).

These two make it possible to view the heap as a regular Python list without surprises: heap[0] is the smallest item, and heap.sort() maintains the heap invariant!

To create a heap, use a list initialized to [], or you can transform a populated list into a heap via function heapify().

heapq.heapify(nums)

heapq.heappush(heap, val)

heapq.heappop(heap) -- pop the smallest one

heapq.heapreplace(heap, val)

class KthLargest(object):
    def __init__(self, k, nums):
        self.window = nums
        self.k = k
        heapq.heapify(self.window) # Transform list x into a heap, in-place, in linear time.
        while len(self.window) > k:
            heapq.heappop(self.window) # Pop and return the smallest item from the heap, maintaining the heap invariant. To access the smallest item without popping it, use heap[0].
    
    # keep a K-size priority queue (heapq in python), and always make it updated and return the smallest of this group, which will be the k-th large element 
    def add(self, val):
        if len(self.window) < self.k:
            heapq.heappush(self.window, val) # Push the value item onto the heap, maintaining the heap invariant
        elif val > self.window[0]: # To access the smallest item without popping it, use heap[0]
            heapq.heapreplace(self.window, val) # This heapreplace operation is more efficient than a heappop() followed by heappush() and can be more appropriate when using a fixed-size heap.
        return self.window[0] # To access the smallest item without popping it, use heap[0]

Max heap in python

What do I use for a max-heap implementation in Python?Stack Overflow

The easiest way is to invert the value of the keys and use heapq. For example, turn 1000.0 into -1000.0 and 5.0 into -5.0.

And you can also use:

import heapq
listForTree = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]    
heapq.heapify(listForTree)             # for a min heap
heapq._heapify_max(listForTree)        # for a maxheap!!

If you then want to pop elements, use:

heapq.heappop(minheap)      # pop from minheap
heapq._heappop_max(maxheap) # pop from maxheap

there IS such a built-in solution in heapq. But then it is totally unreasonable that it is NOT even slightly mentioned at all in the official document! WTF! -- someone

Implement a Heap in Python (by list)

import operator


class Heap(object):
    """"
    Attributes:
        heap: List representation of the heap
        compare(p, c): comparator function, returns true if the relation between p and c is parent-chield
    """
    def __init__(self, heap=None, compare=operator.lt):
        self.heap = [] if heap is None else heap
        self.compare = compare

    def __repr__(self):
        return 'Heap({!r}, {!r})'.format(self.heap, self.compare)

    def _inv_heapify(self, child_index):
        """
        Do heapifying starting from bottom till it reaches the root.
        """
        heap, compare = self.heap, self.compare
        child = child_index
        while child > 0:
            parent = child // 2
            if compare(heap[parent], heap[child]):
                return
            heap[parent], heap[child] = heap[child], heap[parent]
            child = parent

    def _heapify(self, parent_index):
        """
        Do heepifying starting from the root.
        """
        heap, compare = self.heap, self.compare
        length = len(heap)
        if length == 1:
            return
        parent = parent_index
        while 2 * parent < length:
            child = 2 * parent
            if child + 1 < length and compare(heap[child + 1], heap[child]):
                child += 1
            if compare(heap[parent], heap[child]):
                return
            heap[parent], heap[child] = heap[child], heap[parent]
            parent = child

    def del_min(self):
        heap = self.heap
        last_element = heap.pop()
        if not heap:
            return last_element
        item = heap[0]
        heap[0] = last_element
        self._heapify(0)
        return item

    def min(self):
        if not self.heap:
            return None
        return self.heap[0]

    def add(self, element):
        self.heap.append(element)
        self._inv_heapify(len(self.heap) - 1)

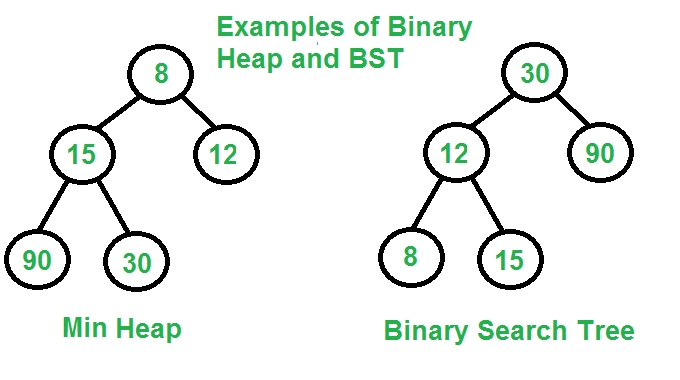
Priority Queue Implementations: Binary Heap or Balanced BST

Why is Binary Heap Preferred over BST for Priority Queue? - GeeksforGeeksGeeksforGeeks

A typical Priority Queue requires following operations to be efficient.

Get Top Priority Element (Get minimum or maximum)
Insert an element
Remove top priority element
Decrease Key

A Binary Heap supports above operations with following time complexities:

O(1)
O(Logn)
O(Logn)
O(Logn)

A Self Balancing Binary Search Tree like AVL Tree, Red-Black Tree, etc can also support above operations with same time complexities.

Finding minimum and maximum are not naturally O(1), but can be easily implemented in O(1) by keeping an extra pointer to minimum or maximum and updating the pointer with insertion and deletion if required. With deletion we can update by finding inorder predecessor or successor.
Inserting an element is naturally O(Logn)
Removing maximum or minimum are also O(Logn)
Decrease key can be done in O(Logn) by doing a deletion followed by insertion. See this for details.

So why is Binary Heap Preferred for Priority Queue?

Since Binary Heap is implemented using arrays, there is always better locality of reference and operations are more cache friendly.
Although operations are of same time complexity, constants in Binary Search Tree are higher.
We can build a Binary Heap in O(n) time. Self Balancing BSTs require O(nLogn) time to construct.
Binary Heap doesn’t require extra space for pointers.
Binary Heap is easier to implement.
There are variations of Binary Heap like Fibonacci Heap that can support insert and decrease-key in Θ(1) time

Is Binary Heap always better? Although Binary Heap is for Priority Queue, BSTs have their own advantages and the list of advantages is in-fact bigger compared to binary heap.

Searching an element in self-balancing BST is O(Logn) which is O(n) in Binary Heap.
We can print all elements of BST in sorted order in O(n) time, but Binary Heap requires O(nLogn) time.
Floor and ceil can be found in O(Logn) time.
K’th largest/smallest element be found in O(Logn) time by augmenting tree with an additional field.

PreviousPython reverse a list NextC++ Notes

Last updated 6 years ago