Kth Largest Element in a Stream

We have introduced the properties of a BST and how to perform the basic operations, including search, insertion and deletion, in a BST. Being familiar with these basic ideas, you will be able to apply a BST to solve a real problem.

The strength of a BST is that you can perform all search, insertion and deletion operations in O(h) time complexity even in the worst case.

Usually, if you want to store data in order and need several operations, such as search, insertion or deletion, at the same time, a BST might be a good choice.

An Example

Problem: Design a class to find the kth largest element in a stream.

A most obvious way to solve this problem is to sort the array in descending order first and then return the kth element in the array.

But we have to sort for the new element every time when we insert a new value in order to perform the search operation in O(1) time complexity. But the time complexity of the insertion operation will be O(N) in average. Therefore, time complexity will be O(N^2) in total.

Since we need insertion and search operations at the same time, what about using a BST to store the values?

As we know, for each node in a BST, all the values in the right subtree are larger than the value of the node itself while all the values in the left subtree are smaller than the value of the node.

In other word, for each node in a BST, if m nodes in the right subtree, the node itself is the m + 1 largest element in the existed array.

Think about the problem by yourself first. Feel free to store more than one value in a tree node. You might also want a counter in each node to indicate how many nodes there are in the subtree rooted at this node.

If you still don't have a clear clue about the solution, we provide the animation of an example for you:

1. Insertion

cur-img

2. Search

cur-img

class KthLargest(object):
    def __init__(self, k, nums):
        self.window = nums
        self.k = k
        heapq.heapify(self.window) # Transform list x into a heap, in-place, in linear time.
        while len(self.window) > k:
            heapq.heappop(self.window) # Pop and return the smallest item from the heap, maintaining the heap invariant. To access the smallest item without popping it, use heap[0].
    
    # keep a K-size priority queue (heapq in python), and always make it updated and return the smallest of this group, which will be the k-th large element 
    def add(self, val):
        if len(self.window) < self.k:
            heapq.heappush(self.window, val) # Push the value item onto the heap, maintaining the heap invariant
        elif val > self.window[0]: # To access the smallest item without popping it, use heap[0]
            heapq.heapreplace(self.window, val) # This heapreplace operation is more efficient than a heappop() followed by heappush() and can be more appropriate when using a fixed-size heap.
        return self.window[0] # To access the smallest item without popping it, use heap[0]

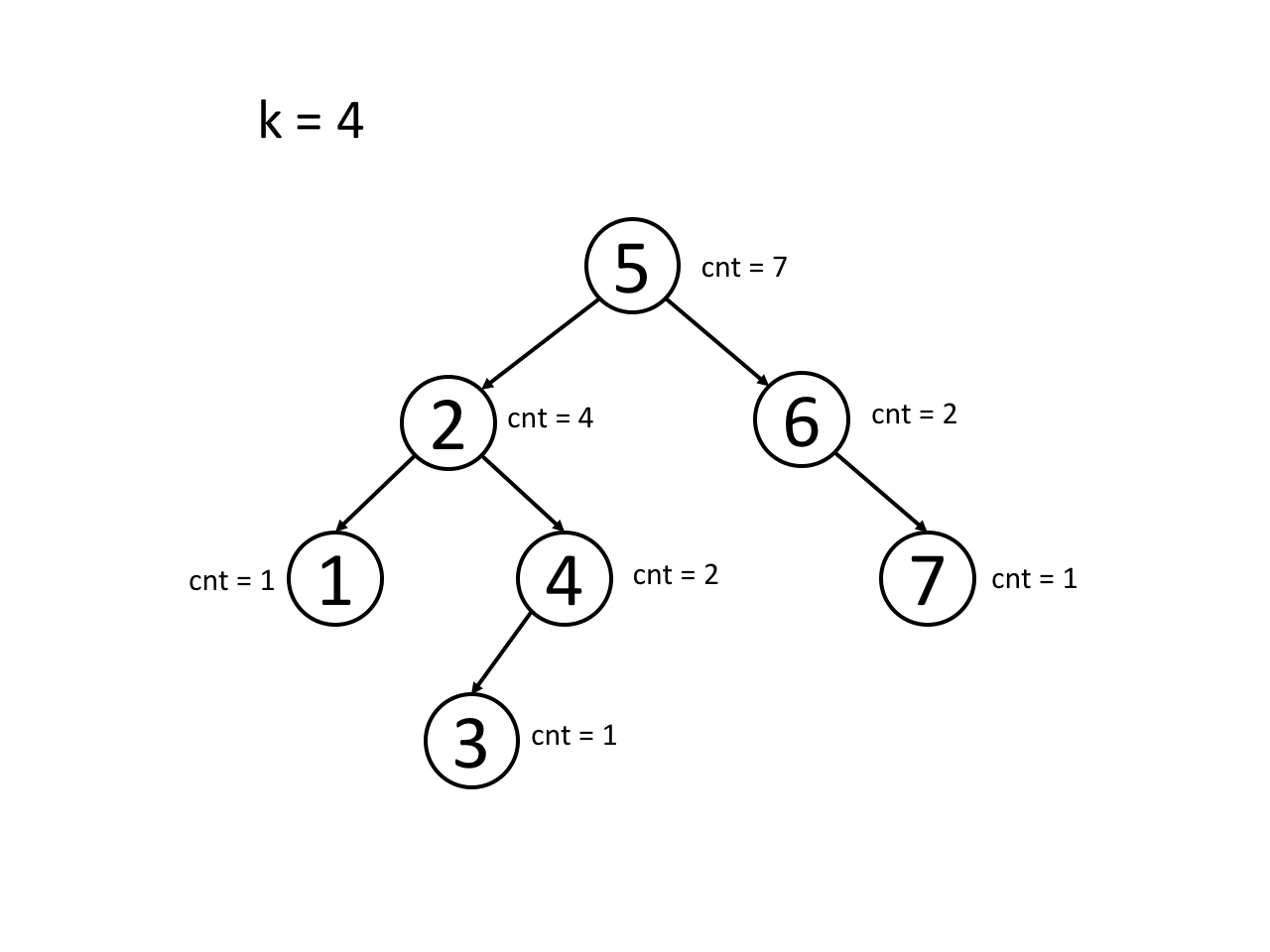
BST solution:

class kthTreeNode(object):
	def __init__(self, x):
		self.val = x
		self.count = 1
		self.left = None
		self.right = None

class KthLargest(object):
    def __init__(self, k, nums):
        self.size = len(nums)
        self.k = k
        if not nums:
        	self.root = None
        else:
            self.root = kthTreeNode(nums[0])
            for i in range(1, len(nums)):
        	    # self.insertNode(nums[i])
                self.insertNodeRecursive(self.root, nums[i])
    
    def insertNode(self, val):
        if not self.root:
            self.root = kthTreeNode(val)
            self.size += 1
            return
    	cur = self.root
    	pre = None
    	while(cur):
    		pre = cur
    		if val < cur.val:
    			cur.count += 1
    			cur = cur.left
    		else:
    			cur.count += 1
    			cur = cur.right
    	if val < pre.val:
    		pre.left = kthTreeNode(val)
    	else:
    		pre.right = kthTreeNode(val)
        self.size += 1
        
    def insertNodeRecursive(self, cur, val):
        if not self.root:
            self.root = kthTreeNode(val)
            self.size += 1
            return self.root
        if not cur:
            self.size += 1
            return kthTreeNode(val)
        if val < cur.val:
            cur.count += 1  # don't forget to add count along the recursive loop
    	    cur.left = self.insertNodeRecursive(cur.left, val)
        else:
            cur.count += 1  # don't forget to add count along the recursive loop
            cur.right = self.insertNodeRecursive(cur.right, val)
        return cur

    def searchKth(self, root, k):
    	while(root):
    		rightCount = 0 if not root.right else root.right.count
    		if k == rightCount + 1: # root 是当前子🌲中 rightCout + 1 大的 node
    			return root.val
    		elif k < rightCount + 1: # k 小于 rightCout + 1 的话，说明 kth node 在右支中
    			return self.searchKth(root.right, k)
    		else: # k 大于 rightCount + 1 的话，说明 kth node 在左支中，且 kth node 变为左支子树里 (k - (rightCount + 1))th node，然后迭代进行
    			return self.searchKth(root.left, k - rightCount - 1)

    def add(self, val):
    	# self.insertNode(val)
        self.insertNodeRecursive(self.root, val)
    	return self.searchKth(self.root, self.k)