General Introduction

DFS is the basic method for solving various problems, such as recursion, backtrack, graph search, even for many brutal force algorithms.

Intro

Graph DFS is similiar to Tree DFS, because Tree is a special kind of Graph

Main idea: suppose that the initial state of each node in the graph is 'Not visited yet'. And we will start the searching from some node v, and visit it first , then visit its neighbor nodes via depth first criterion, until all nodes connected to v have been visited. If there are still nodes haven't been visited, we will choose another node, besides v, as start node to do the same thing again. Repeat until all nodes are visited.

Obviously, DFS is a recursive process.

Understand it

DFS Implementation

Since tree can be treated as a graph, we will use graph to implement DFS

public calss GraphNode{
  int val;
  List<GraphNode> neighnors;
}

To avoid duplicates, use a hash map to save the visited nodes.

HashSet<GraphNode> visited = new HashSet<GraphNode>();

Recursive DFS

Once meet a node, mark it visited and do DFS for its neighbors

public void DFS(GraphNode nd){
  //print nd.val
  visited.add(nd);
  for(GraphNode next : nd.neighbours){
    if(!visited.contains(next)){
      DFS(next);
    }
  }
}

Non-recursive DFS

non-recursive version is more efficient than recursive one.

public void DFS(GraphNode start){
  Stack<GraphNode> s = new Stack<GraphNode>();
  q.push(start);
  visited.add(start);
  while(!s.empty()){
    GraphNode cur = s.pop();
    //print cur.val
    for(GraphNode next : cur.children){
      if(!visited.contains(next)){
        s.push(next);
        visited.add(next);//mark node as visited when adding to stack.
      }
    }
  }//while end
}

Cycle Detection

对DFS稍作修改，可以判断一个有向图是否有回路

在递归版本里，我们队每一个点改为三种标记：

• 未访问过(0)

• 正在访问其邻居节点(1)

• 已经访问完毕该节点以及所有该节点可以到达的节点(2)

什么时候会出现回路？就是当前节点v的一个邻居u的状态为1的时候。

因为该节点状态为1，即还没有把它以后的节点全部遍历，所以当前节点v肯定可以从u到达，而现在又可以从v到达u，所以回路构成。

为了表示一个节点的三种状态, 我们把visited的定义改一下, 定义为一个hashmap: HasheMap visited = new HasheMap();

节点不在visited表示还未访问过, 节点对应为false表示正在访问, 节点对应为true表示已经访问该节点以及所有可以从它到达的节点.

public void DFS(GraphNode nd){      
    visited.put(nd, false); // mark as status-1   
    for(GraphNode next: nd.neighbors){   
        if( !visited.contains(next) )   
            DFS(next);   
        else if(visited.get(next)==false) // found cycle   
            System.out.println("Cycle detected!!!");   
    }// now all touchable nodes from nd are visited   
    visited.put(nd, true); // mark as status-2   
}

Topology Sort

这一节(以及上一节)参考这个非常棒的视频: https://class.coursera.org/algo-003/lecture/52

拓扑排序是一个dfs的应用, 所谓拓扑排序是指在一个DAG(有向无回路图)里给每个节点定义一个顺序(v1…vn), 使得按照这个顺序遍历的节点, 每一个节点vi都是之前遍历过的的节点(v1 ~ vi-1)所指向的(或没有任何其他节点指向的).

好像还没说清楚… 拓扑排序的一个应用就是对于各种依赖性(比如学习课程A需要先学习过课程B)组成的图寻找一个节点遍历的顺序使其可行.

propositions:

• 拓扑排序的结果不唯一.

• 有回路的图不存在拓扑顺序.

• 如果一个节点没有出边, 那么它可以放在拓扑排序的最后面(没有节点以来它).

• 如果一个节点没有入边, 那么它可以放在拓扑排序的最后面.

简单修改一下递归的dfs就可以处理拓扑排序: 维护一个计数器K(初始化为n=所有节点数), 每当一个点已经遍历完毕(所有通过这个点可以到达的点都已经被走过)以后, 就把这个点的顺序设为K, 同时减少K.

就用一个HashMap来为每个节点关联一个序号好了: HasheMap order = new HasheMap();

public void DFS(GraphNode nd){      
    for(GraphNode next: nd.neighbors){   
        if( !visited.contains(next) )   
            DFS(next);   
    }// all touchable nodes from nd are visited   
    order.put(nd, K--);   
}

Detect Cycle in a Directed Graph

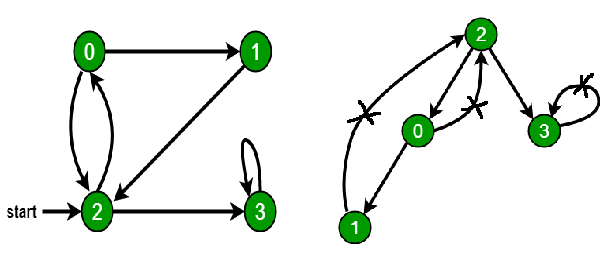
Given a directed graph, check whether the graph contains a cycle or not. Your function should return true if the given graph contains at least one cycle, else return false. For example, the following graph contains three cycles 0->2->0, 0->1->2->0 and 3->3, so your function must return true.

Depth First Traversal can be used to detect a cycle in a Graph. DFS for a connected graph produces a tree. There is a cycle in a graph only if there is a back edge present in the graph. A back edge is an edge that is from a node to itself (self-loop) or one of its ancestor in the tree produced by DFS. In the following graph, there are 3 back edges, marked with a cross sign. We can observe that these 3 back edges indicate 3 cycles present in the graph.

For a disconnected graph, we get the DFS forest as output. To detect cycle, we can check for a cycle in individual trees by checking back edges.

To detect a back edge, we can keep track of vertices currently in recursion stack of function for DFS traversal. If we reach a vertex that is already in the recursion stack, then there is a cycle in the tree. The edge that connects current vertex to the vertex in the recursion stack is a back edge. We have used recStack[] array to keep track of vertices in the recursion stack.

# Python program to detect cycle  
# in a graph 
  
from collections import defaultdict 
  
class Graph(): 
    def __init__(self,vertices): 
        self.graph = defaultdict(list) 
        self.V = vertices 
  
    def addEdge(self,u,v): 
        self.graph[u].append(v) 
  
    def isCyclicUtil(self, v, visited, recStack): 
  
        # Mark current node as visited and  
        # adds to recursion stack 
        visited[v] = True
        recStack[v] = True
  
        # Recur for all neighbours 
        # if any neighbour is visited and in  
        # recStack then graph is cyclic 
        for neighbour in self.graph[v]: 
            if visited[neighbour] == False: 
                if self.isCyclicUtil(neighbour, visited, recStack) == True: 
                    return True
            elif recStack[neighbour] == True: 
                return True
  
        # The node needs to be poped from  
        # recursion stack before function ends 
        recStack[v] = False
        return False
  
    # Returns true if graph is cyclic else false 
    def isCyclic(self): 
        visited = [False] * self.V 
        recStack = [False] * self.V 
        for node in range(self.V): 
            if visited[node] == False: 
                if self.isCyclicUtil(node,visited,recStack) == True: 
                    return True
        return False
  
g = Graph(4) 
g.addEdge(0, 1) 
g.addEdge(0, 2) 
g.addEdge(1, 2) 
g.addEdge(2, 0) 
g.addEdge(2, 3) 
g.addEdge(3, 3) 
if g.isCyclic() == 1: 
    print "Graph has a cycle"
else: 
    print "Graph has no cycle"